Introduction to Pericyclic Reactions

  1. Reaction classes
  2. Pericyclic reaction types
    1. Cycloadditions
    2. Electrocyclic reactions
    3. Sigmatropic rearrangements
  3. General features of pericyclic reactions
    1. Cycloadditions
    2. Electrocyclic reactions
    3. Sigmatropic rearrangements
  4. Mechanistic analysis of pericyclic reactions
  5. Frontier molecular orbitals and interaction diagrams
    1. The C–H bond
    2. The C–C σ bond
    3. The C–C π bond
    4. The π orbitals of 1,3-butadiene
    5. The π orbitals of allyl (propenyl) anion and cation
  6. Electron distribution in covalent bonds
  7. Describing reactions as HOMO–LUMO interactions

1 Reaction classes

In the broadest sense there are three reaction classes, characterised by the way that the electrons behave in reaction mechanisms. Ionic reactions, the most common, involve charge build-up, with electron pairs moving in one direction under the influence of various structural features. The electron pair movements involved in bond making and bond breaking may be synchronous, as in the SN2 reaction, or stepwise, as in electrophilic additions to alkenes, but the driving forces are the same — electron deficiency (electrophilicity, acidity, oxidation potential, etc.) or electron excess (nucleophilicity, basicity, reduction potential). Radical reactions differ in that they proceed through a stepwise redistribution of single, rather than paired, electrons. Such reactions are also driven by structural factors, particularly hypovalency, but proceed without the (necessary) build-up of charge.

The third distinct reaction class is pericyclic reactions. A working definition is a reaction that takes place as a continuous, concerted reorganisation of electrons. Pericyclic reactions are distinct in proceeding through cyclic transition structures in which the participating molecular orbitals (MOs) maintain bonding interactions throughout. Pericyclic reactions are commonly represented using curly arrows, but it will soon be obvious that this is deceptive — the bonding changes in a pericyclic reaction might be represented using arrows, but any impression of pairwise movement in one direction is false. In a pericyclic reaction, the MOs of the starting material(s) smoothly evolve into the MOs of the product(s).

We will see later how Woodward and Hoffmann reached the conclusion that this 'evolution' must take place with the conservation of orbital symmetry, i.e. each starting MO correlates with a product MO that possesses the same symmetry properties.

2 Pericyclic reaction types

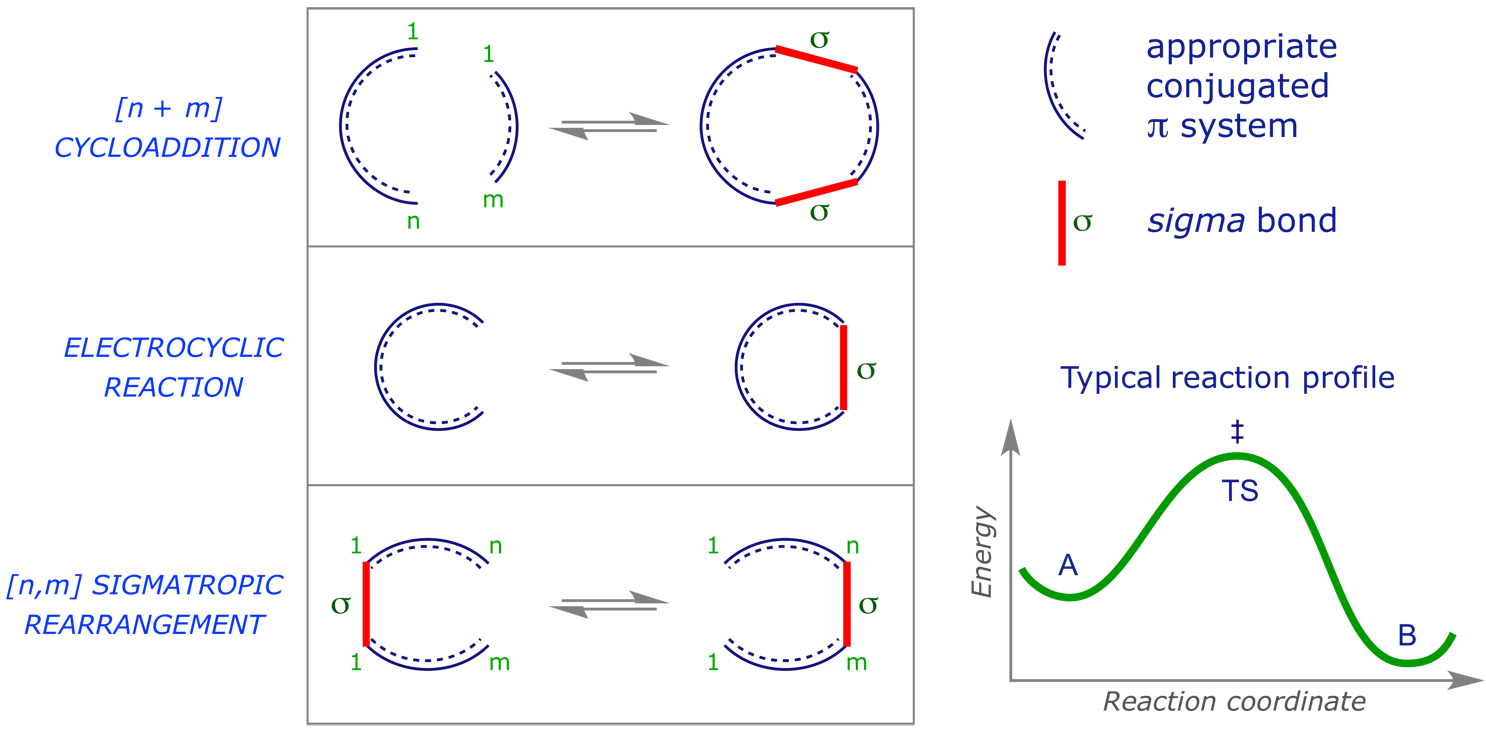
We will consider three major sub-classes of pericyclic reaction, illustrated below in schemes showing both the 'deceptive' mechanistic arrows and a representation of the characterising cyclic transition structure.

2.1 Cycloadditions

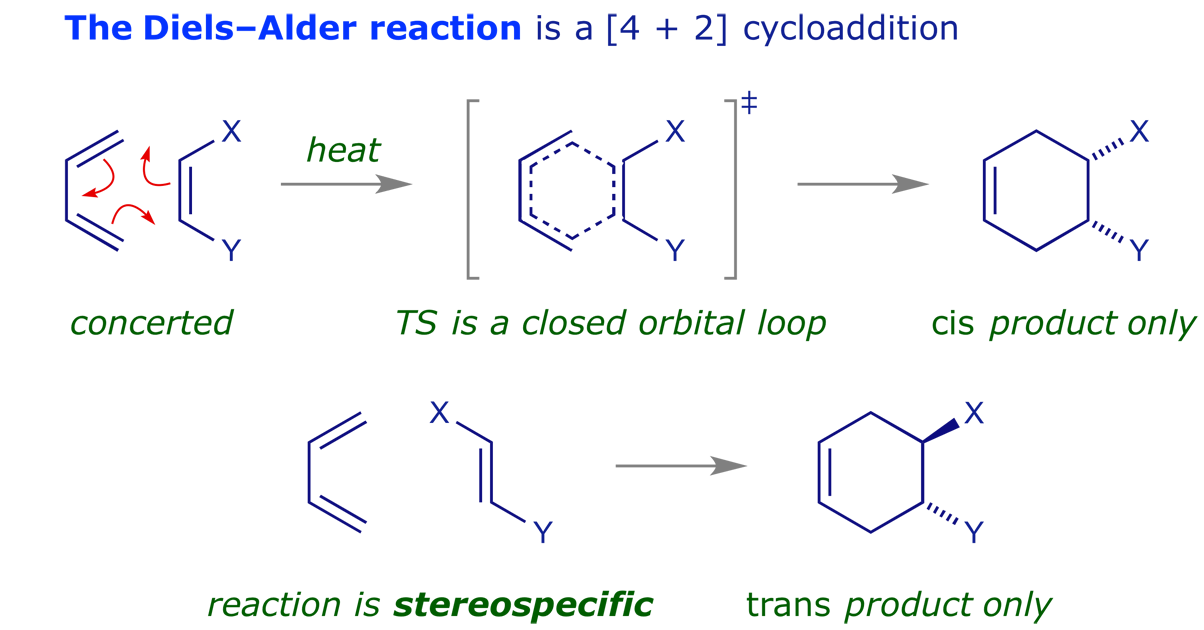
These are pericyclic reactions in which two pi-components combine to generate a new ring through the formation of two new sigma-bonds. Such reactions are usually stereospecific, with the stereochemistry of the starting materials determining that of the products.

Scheme showing the Diels-Alder cycloaddition

2.2 Electrocyclic reactions

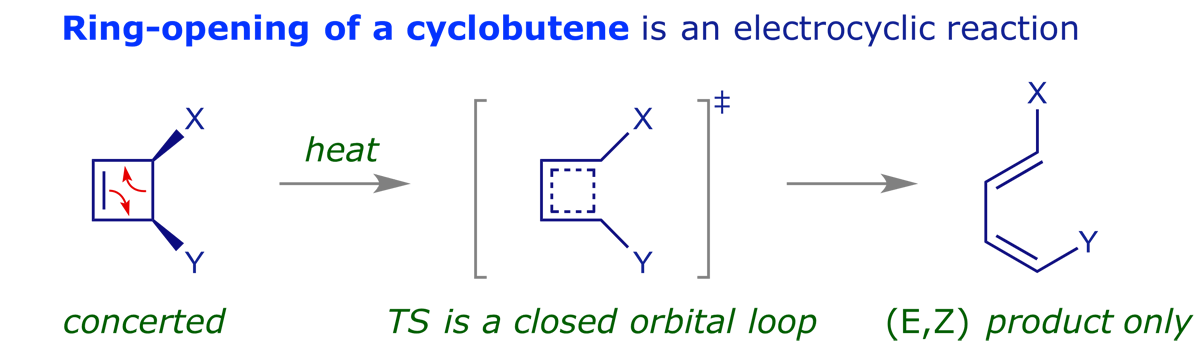
These are pericyclic reactions in which a ring is opened (or closed) through the conversion of a sigma-bond into a pi-bond (or the reverse).

Scheme showing the electrocylic ring opening of a cyclobutene

2.3 Sigmatropic rearrangements

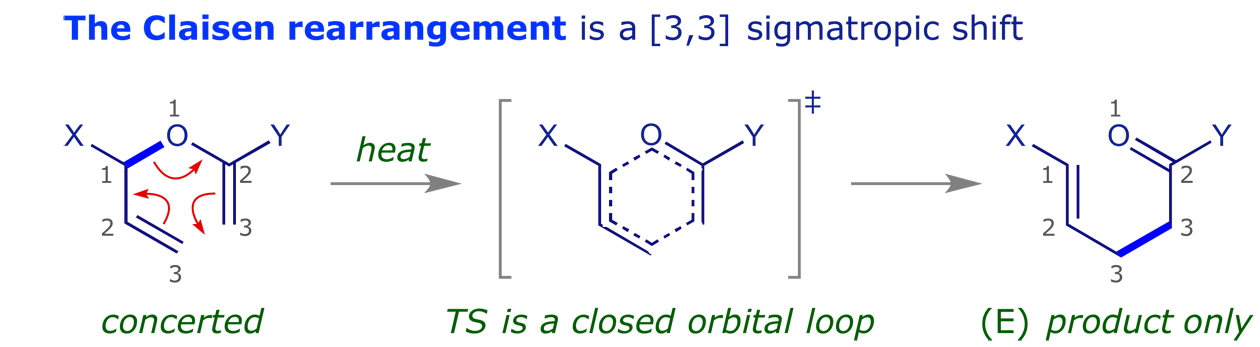
These are pericyclic reactions in which a sigma bond 'appears to move' across a conjugated system to a new site.

Scheme showing the Claisen rearrangement

3 General features of pericyclic reactions

Pericyclic reactions have been known for over 100 years, and can be highly, even fully, selective, making them valuable in synthesis. They have the following general features:

The main types of pericyclic reaction

All of these reactions are subject to strict selection rules whose origin will become clear when FMO principles are applied and the following interrelated factors taken into account:

The last of these points is particularly important — pericyclic reactions are stereospecific. This is what makes them so valuable in synthesis, and generations of chemists have investigated the reaction mechanisms. The examples below illustrate some of the intriguing possibilities.

3.1 Cycloadditions

[4 + 2] Cycloaddition of 1,3-butadiene to maleic anhydride
Photoaddition of ethene to maleic anhydride
Diels-Alder dimerisation of cyclopentadiene

3.2 Electrocyclic reactions

Thermal electrocyclic ring-closure of (E,Z,E)-2,4,6-octatriene
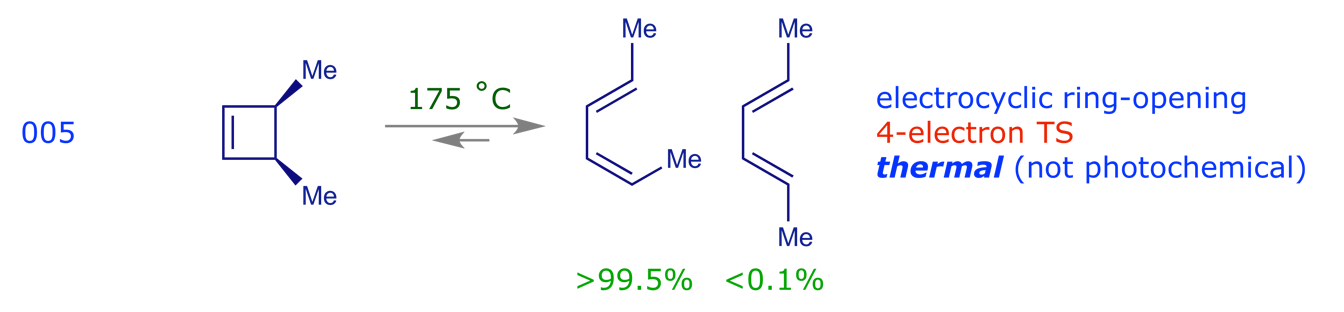
Thermal electrocyclic ring-opening of cis-3,4-dimethylcyclobutene
Photochemical electrocyclic ring-closure of (E,E)-2,4-hexadiene

3.3 Sigmatropic rearrangements

Suprafacial 1,5-hydrogen shifts in cyclopentadienes
[3,3] Claisen rearrangement of allyloxybenzene
[3,3] Sigmatropic (oxy-Cope) rearrangement of 1,2-divinylcyclohexanol

4 Mechanistic analysis of pericyclic reactions

The underlying principles of pericyclic reactions have emerged in various forms, and we will focus on the frontier molecular orbital (FMO) approach developed by Fukui in the 1950s. This allows the interpretation of a molecular interaction to be restricted to an analysis of the interactions between the highest occupied and lowest unoccupied molecular orbitals (HOMOs and LUMOs) of the reacting partners.

Photo of Kenji Fukui
Kenichi Fukui
1918–1998
Nobel Prize 1981
Photo of Robert Woodward
Robert Burns Woodward
1917–1979
Nobel Prize 1965
Photo of Raold Hoffmann
Raold Hoffmann
b. 1937
Nobel Prize 1981

The underlying principles of pericyclic reactions have emerged in various forms, and we will focus on the frontier molecular orbital (FMO) approach developed by Fukui in the 1950s. This allows the interpretation of a molecular interaction to be restricted to an analysis of the interactions between the highest occupied and lowest unoccupied molecular orbitals (HOMOs and LUMOs) of the reacting partners.

Other important theories and interpretations that will be touched upon include the following:

Conservation of orbital symmetry (Woodward-Hoffmann):  This is the first theory that successfully explained and predicted the outcome of pericyclic reactions. It correlates all the relevant orbitals in the starting material(s) and product(s). We will see a few examples of the vehicle for this type of analysis, the orbital correlation diagram, but we won't need to go too deeply the theory.

Aromatic transition structure (Dewar-Zimmerman):  This is an easy concept to apply to all reaction types, but it's not so easy to understand why it is valid, especially in comparison with the FMO approach that we will generally choose.

We will begin with some revision of the principles and terminology of covalent bonding, with an emphasis on π systems.

5 Frontier molecular orbitals and interaction diagrams

Molecular orbitals are constructed by the linear combination of atomic orbitals (LCAO) method. This topic is revised here so that the key features of FMOs, namely their energy and symmetry properties, can be called upon during our mechanistic analysis of pericyclic reactions. It is useful to know how to draw the HOMOs and LUMOs of π systems.

5.1 The C–H bond

Using the LCAO method, we can construct a diagram showing the possible combinations of a hydrogen 1s orbital and a carbon sp3 hybrid orbital to provide a picture of a C–H σ bond such as those in methane. This will serve our purposes but should be recognised as deceptive, as methane has eight valence electrons and hence four MOs. We have used hybridisation to 'mix' them and simplify the picture.

MO diagram for a C-H sigma bond

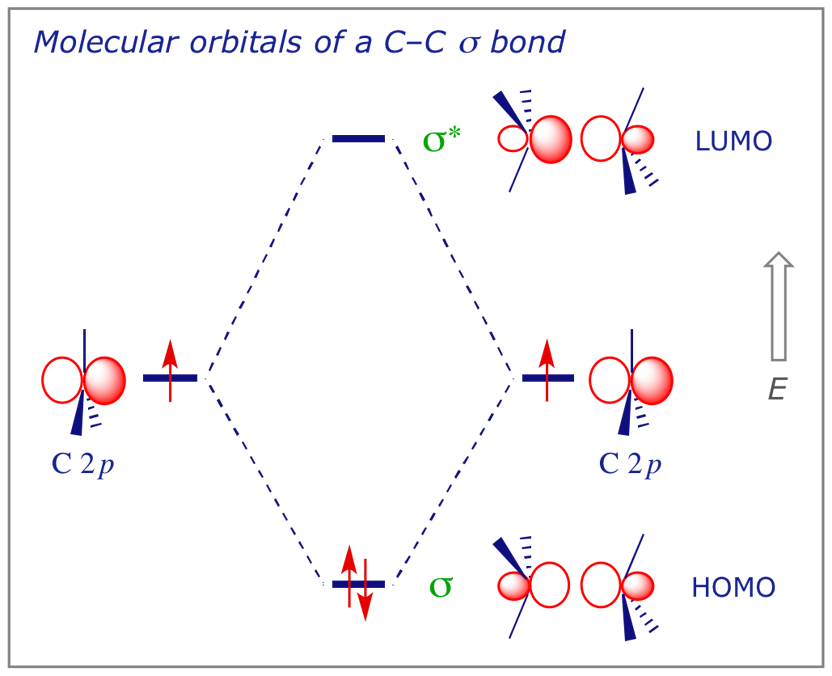
5.2 The C–C σ bond

In ethane there are 14 valence electrons, and therefore 7 filled MOs, but we will again simplify the picture. The interaction diagram below will be used to represent the most significant orbital interactions that contribute to a C–C σ (sigma) bond.

MO diagram for a C-C sigma bond

5.3 The C–C π bond

Orbital coefficients

The electron distribution function ψ for a molecular orbital is the sum of the atomic orbitals which contribute, i.e.

$$ \psi_{_{\text{MO}}} \ = \sum \textit{c}_{i}\phi _{i} $$

where the coefficient c is a measure of the contribution that each atomic orbital makes to the molecular orbital. For a C=C π bond the bonding (π) and antibonding (π*) combinations are thus:

$$\begin{align*} \pi \ \ &= \ \textit{c}_{1}\phi _{1} + \textit{c}_{2}\phi _{2} \\ \pi^{*} \ &= \ \textit{c}_{1}\phi _{1} - \textit{c}_{2}\phi _{2} \end{align*}$$

The squares of the c values are a measure of the electron population in the neighbourhood of the atom in question. Only one electron in each spin state can be in each orbital, so the following must be true:

$$ \sum c^{2} \ = \ \text{1} $$

For a symmetrical C=C π bond the c values must be the same, so the π and π* combinations become:

$$\begin{align*} \pi \ \ &= \ \text{0.7071}\phi _{1} + \text{0.7071}\phi _{2} \\ \pi^{*} \ &= \ \text{0.7071}\phi _{1} - \text{0.7071}\phi _{2} \end{align*}$$

The molecular orbital for the π (pi) bond in ethene is higher in energy than the (five) other occupied MOs and the system can be represented by the diagram below, showing the possible combinations of two carbon 2p atomic orbitals. It should be borne in mind that π bonding, with its 'sideways' overlap, is inherently weaker than sigma bonding, so both the drop in energy due to bonding and the HOMO-LUMO energy gap are lower for this type of bond.

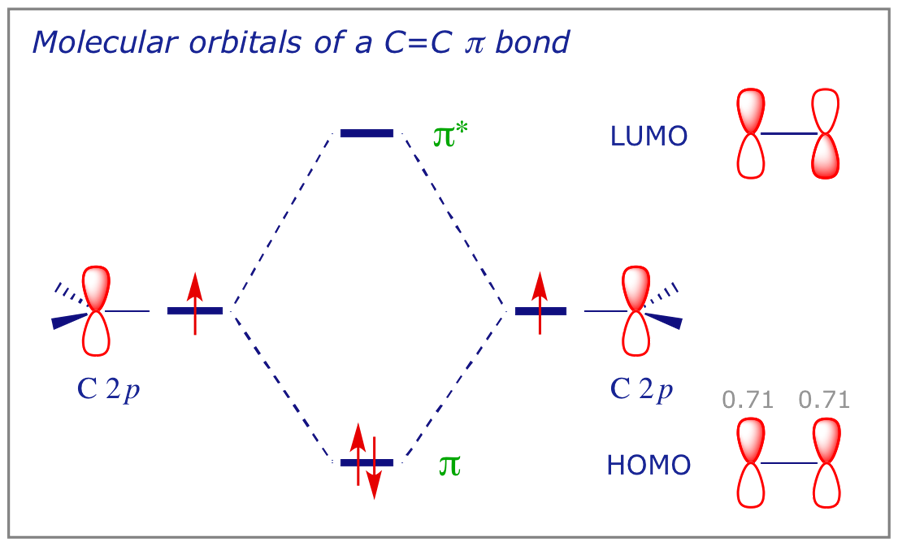
MO diagram for a C=C pi bond

The C 2p orbital is the highest energy orbital on an sp2 carbon, so this diagram actually shows the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO) of ethene. These are the frontier molecular orbitals (FMOs) of the molecule.

5.4 The π orbitals of 1,3-butadiene

Combining four carbon 2p orbitals provides us with the molecular orbitals of 1,3-butadiene. In order of increasing energy, these have zero, 1, 2 and 3 nodes. The total of four electrons fill the two lowest π MOs, so the HOMO and LUMO are ψ2 and ψ3 respectively. The c values vary between two values in this system, although for most purposes it is only required that a diagram correctly depicts the relative phases. The MOs of higher conjugated polyenes, e.g. 1,3,5-hexatriene, are easily constructed by extending the same LCAO approach.

MO diagram for the pi bonds of butadiene

5.5 The π orbitals of allyl (propenyl) anion and cation

The allyl cation, allyl anion and allyl radical all have the same orbitals, but each system contains a different number of electrons. We can construct the MO of the allyl system by the linear combination of a C=C π bond (made from two C 2p orbitals) with a third C 2p orbital, as below. Notice that, compared with the C=C π bond, the energies of both the HOMO and the LUMO are lower in the allyl cation and higher in the allyl anion. The significance of this will become more obvious in the context of perturbation by substituent effects (see later). In the allyl radical, ψ2 is a singly-occupied molecular orbital (SOMO).

MO diagram for allyl anion
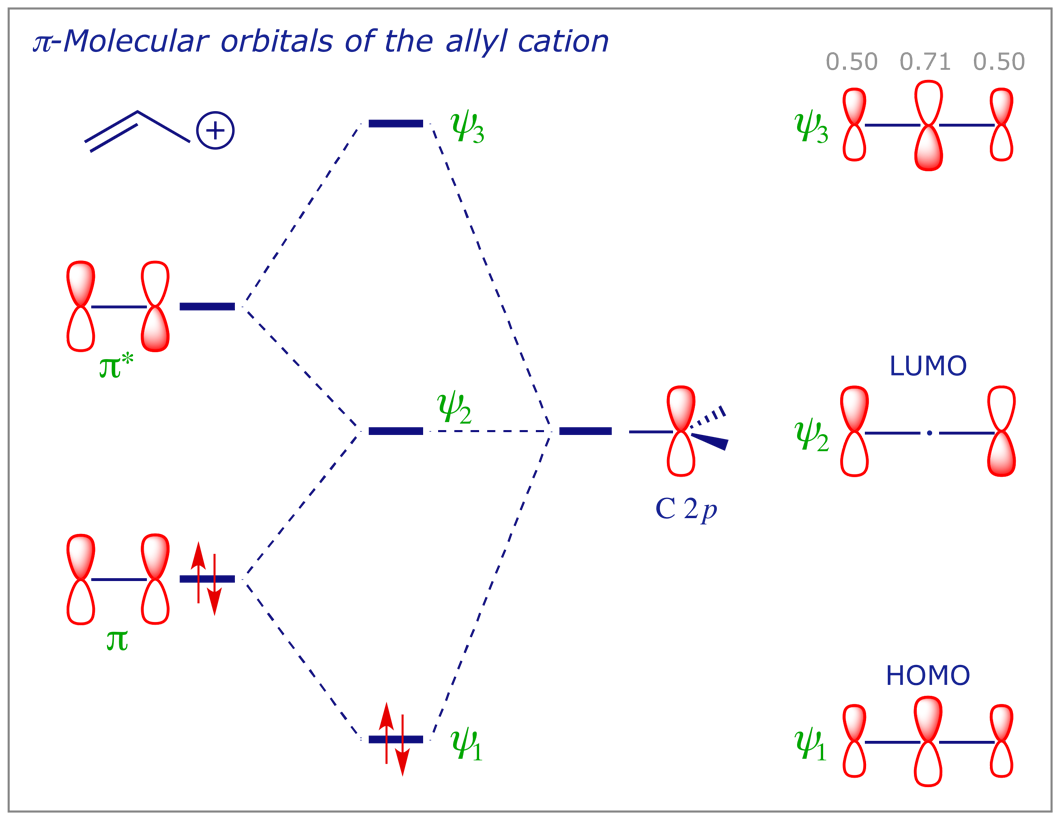
MO diagram for allyl cation

6 Electron distribution in covalent bonds

In ethene the lobes of the π bond have the same size (the two C 2p AOs contribute equally to the MO). This is not the case in an unsymmetrical covalent bond, since the electron distribution is subject to the different influences of each contributing atom. Unless a covalent bond is completely symmetrical, its electron density will tend to be polarised. This is a manifestation of ionic character, and the limiting case is, of course, a fully ionic bond.

A comparison of the C=C and C=O π bonds illustrates this in terms of MO energies. We constructed the orbital interaction diagram for a C=C π bond (see 5.3). The diagram for a C=O π bond is similar, but this time the two orbitals involved are not the same.

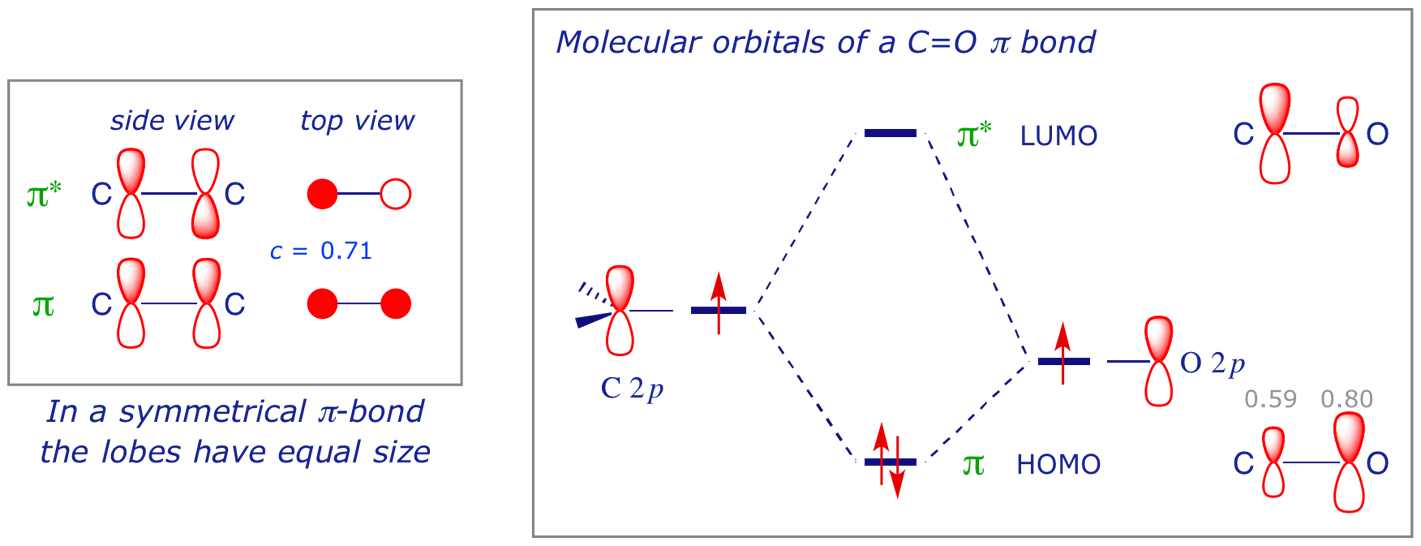
MO diagrams for a C=O pi bond

The following points should be borne in mind when considering orbital interactions:

  1. When the interacting orbitals are close in energy, the interaction is larger.
  2. When the overlap of the orbitals is larger, the interaction is larger.
  3. When orbitals of different energies interact, the molecular orbital (MO) contains more of the atomic orbital (AO) which is closer to it in energy.

The last of these points is important when comparing C=C with C=O. There is uneven electron distribution in the C=O orbitals (the c values are unequal): O has more electron density in πC=O whereas C has more in π*C=O. As well as the bonded atoms themselves, double bond substituents can induce uneven distribution of electron density in π systems. This is particularly significant in the context of the [4π + 2π] (Diels-Alder) cycloaddition (see 1.3).

7 Describing reactions as HOMO–LUMO interactions

We can use orbital interaction diagrams to describe the bonding stabilisation that occurs in a transition structure when two different atoms join to form a new bond, and using the same principles it is possible to construct an orbital interaction diagram for two reacting molecules. The starting point for this is the recognition that, as two molecules approach, three major forces operate:

HSAB
In hard/soft acid/base terms, the situation in (2) drives the hard-hard interaction (ionic bonding). The situation in (3) describes the soft-soft interaction (covalent bonding).

  1. The occupied orbitals of one molecule repel the occupied orbitals of the other. This is known as filled shell repulsion.
  2. Any positive charge on one molecule attracts any negative charge on the other (and repels any positive). This is Coulombic attraction.
  3. The occupied orbitals (especially the HOMOs) of each molecule interact with the unoccupied orbitals (especially the LUMOs) of the other, causing an attraction between the molecules. The interaction is greatest when the interacting HOMO and LUMO are close in energy.

The HOMO-LUMO interaction is particularly important for pericyclic reactions, and is quantified in the third (frontier orbital) term of the Klopman-Salem equation. Klopman and Salem showed that a chemical reaction can be analysed in orbital terms by summing the interactions 1–3 above for whole molecules when they approach each other (perturbation theory). Their equation contains separate expressions for the electrostatic and covalent interactions between two molecules, which can be of the bonding type (unlike-charge ionic and filled-empty covalent) or the repulsion type (like-charge ionic or filled-shell repulsions).

An equation for estimating chemical reactivity

The energy (ΔE) gained and lost when the orbitals of one reactant overlap with those of another can be expressed in the following equation, developed by Klopman and Salem using Perturbation Theory:

$$ \Delta E \ = \ -\sum (q_{a}+q_{b})\beta _{ab}S_{ab} \ + \sum_{k< l}\ \frac{Q_{k}Q_{l}}{\varepsilon R_{kl}} \ +\left ( \sum_{r}^{occ.}\sum_{s}^{unocc.}\ - \sum_{s}^{occ.}\sum_{r}^{unocc.}\frac{2\left ( \sum_{a,b} c_{ra}c_{sb}\beta_{ab} \right )^{2}} {E_{r}-E_{s}}\right ) $$

where
qa and qb are the electron populations in the atomic orbitals a and b
β and S are resonance and overlap integrals
Qk and Ql are the total charges on atoms k and l
ε is the local dielectric constant
Rkl is the distance between the atoms k and l
cra is the coefficient of atomic orbital a in molecular orbital r, where r refers to the molecular orbitals on one molecule and s refers to those on the other
Er is the energy of molecular orbital r

The Klopman-Salem equation can be simplified by assuming that the only significant covalent interactions are those between the HOMOs and LUMOs (the frontier orbitals) of the two interacting molecules, other covalent interactions being ignored on the basis of their larger energy gaps (i.e. values for Er − Es). The simplified equation for chemical reactivity includes terms for quantifying the coulombic (ionic) and frontier orbital (covalent) interactions of two molecules:

$$ \Delta E \ = \ - \ \frac{Q_{nuc}Q_{elec}}{\varepsilon R}\ + \ \frac{2\left ( c_{nuc}c_{elec}\beta \right )^{2}}{E_{HOMO(nuc)}-E_{LUMO(elec)}} $$

Note that the frontier orbital term will be dependent on the coefficients (sizes) of the overlapping orbitals, the extent of the orbital overlap, and the energy difference between the interacting HOMOs and LUMOs.